Understanding the CNN equations of backpropagation
In the course of this article I will use convolution in place of the technically more correct cross correlation to match the convention in ML
During my first search for the equations of backpropagation for convolutional neural networks I was faced with one of two outcomes.
The first gave me the slick
$$\frac{\partial L}{\partial X} = \operatorname{Conv}\left(\operatorname{Pad}\left(\frac{\partial L}{\partial Z}\right), K_{rot 180\degree}\right)$$ $$\frac{\partial L}{\partial K} = \operatorname{Conv}\left(X, \frac{\partial L}{\partial Z}\right)$$ $$\frac{\partial L}{\partial b} = \operatorname{Sum}\left(\frac{\partial L}{\partial Z}\right)$$with absolutely no understanding or intuition about how this followed from the underlying chain rule calculations.
The second kind of answer was a wild mess of nested sums, indices, subscripts, and superscripts that - while more obviously followed from the calculus - provides little help for our feeble brains to understand what operations were actually being done.
This blog is an attempt to bridge the two by running through a (very) small in dimension convolutional layer.
One small convolutional layer
Let us focus on a convolutional layer with only one input and one output channel i.e. one flat 2-d kernel. The same idea easily extends to more kernels and more input channels - this is to avoid a mess of notation with lots of indices.
Say we have an 3x3 input image with one channel $X$, a 2x2 kernel $K$, and a bias $b$. Then denote their elements by
$$X = \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \\ \end{bmatrix} ,\;\; K = \begin{bmatrix} k_{11} & k_{12} \\ k_{21} & k_{22} \\ \end{bmatrix} ,\;\; Z = \operatorname{Conv}(X, K) + b = \begin{bmatrix} z_{11} & z_{12} \\ z_{21} & z_{22} \\ \end{bmatrix}. $$Now we want to see how error is propagated backwards through this layer - i.e. find $\frac{\partial L}{\partial K}$, $\frac{\partial L}{\partial b}$, and $\frac{\partial L}{\partial X}$ to work out how to update the weights, bias, and propagate the error to the layer behind respectively.
Now as we are looking at just one intermediate layer in the chain of layers that make up a CNN assume we have the error in the outputs $\frac{\partial L}{\partial Z}$ from the backpropagation through the layer directly down the chain from this one.
Finding $\frac{\partial L}{\partial K}$
Lets proceed by finding the loss with respect to a single weight in the kernel.
Unpacking the convolution operation, we see that each $z_{ij}$ is a function of all of the weights in the kernel. e.g. $z_{11} = k_{11}x_{11} + k_{12}x_{12} + k_{21}x_{21} + k_{22}x_{22} + b$
So - remembering that each $k_{mn}$ affects every $z_{ij}$ - using the chain rule for partial derivatives we get
$$ \left(\frac{\partial L}{\partial K}\right)_{mn} = \frac{\partial L}{\partial K_{mn}} = \sum_{i,j} \frac{\partial L}{\partial Z_{ij}}\frac{\partial Z_{ij}}{\partial K_{mn}} $$This makes sense when thinking about the connections in the network, each $k_{mn}$ has many routes to influence the loss.
e.g. $k_{11}$ is used in the calculation of $z_{11}$ which affects all the following layers and then the loss. But $k_{11}$ is also used in the calculation $z_{12}$ and $z_{21}$ and $z_{22}$, each of which affect the loss down the chain as well.
So we need to sum up the contributions to the loss from each of these pathways to get the full picture about how the loss is affected by a single weight.
Writing these equations out in the case of our example we get:
$$\begin{aligned} \frac{\partial L}{\partial K_{11}} = \frac{\partial L}{\partial Z_{11}} \cdot x_{11} + \frac{\partial L}{\partial Z_{12}} \cdot x_{12} + \frac{\partial L}{\partial Z_{21}} \cdot x_{21} + \frac{\partial L}{\partial Z_{22}} \cdot x_{22} = \begin{bmatrix} x_{11} & x_{12} & \phantom{x_{13}}\\ x_{21} & x_{22} & \phantom{x_{23}}\\ \phantom{x_{31}} & \phantom{x_{32}} & \phantom{x_{33}} \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}}\\ \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} \end{bmatrix} \\ \frac{\partial L}{\partial K_{12}} = \frac{\partial L}{\partial Z_{11}} \cdot x_{12} + \frac{\partial L}{\partial Z_{12}} \cdot x_{13} + \frac{\partial L}{\partial Z_{21}} \cdot x_{22} + \frac{\partial L}{\partial Z_{22}} \cdot x_{23} = \begin{bmatrix} \phantom{x_{11}} & x_{12} & x_{13}\\ \phantom{x_{21}} & x_{22} & x_{23}\\ \phantom{x_{31}} & \phantom{x_{32}} & \phantom{x_{33}} \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}}\\ \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} \end{bmatrix} \\ \frac{\partial L}{\partial K_{21}} = \frac{\partial L}{\partial Z_{11}} \cdot x_{21} + \frac{\partial L}{\partial Z_{12}} \cdot x_{22} + \frac{\partial L}{\partial Z_{21}} \cdot x_{31} + \frac{\partial L}{\partial Z_{22}} \cdot x_{32} = \begin{bmatrix} \phantom{x_{11}} & \phantom{x_{12}} & \phantom{x_{13}}\\ x_{21} & x_{22} & \phantom{x_{23}}\\ x_{31} & x_{32} & \phantom{x_{33}} \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}}\\ \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} \end{bmatrix} \\ \frac{\partial L}{\partial K_{22}} = \frac{\partial L}{\partial Z_{11}} \cdot x_{22} + \frac{\partial L}{\partial Z_{12}} \cdot x_{23} + \frac{\partial L}{\partial Z_{21}} \cdot x_{32} + \frac{\partial L}{\partial Z_{22}} \cdot x_{33} = \begin{bmatrix} \phantom{x_{11}} & \phantom{x_{12}} & \phantom{x_{13}}\\ \phantom{x_{21}} & x_{22} & x_{23}\\ \phantom{x_{31}} & x_{32} & x_{33} \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}}\\ \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} \end{bmatrix} \end{aligned} $$With the last line formatted as such to make it easier to spot that this whole operation is in fact a convolution of the input with $\frac{\partial L}{\partial Z}$ i.e.
$$ \operatorname{Conv} \left( \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{bmatrix} ,\; \begin{bmatrix} \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}} \\ \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} \end{bmatrix} \right) $$So we have found that
$$\frac{\partial L}{\partial K} = \operatorname{Conv}\left(X, \frac{\partial L}{\partial Z}\right)$$Finding $\frac{\partial L}{\partial B}$
Finding the gradient with respect to the bias is much simpler. Expanding out the convolution operation to calculate $Z$ we get
$$ \begin{aligned} z_{11} = k_{11}x_{11} + k_{12}x_{12} + k_{21}x_{21} + k_{22}x_{22} + b\\ z_{12} = k_{11}x_{12} + k_{12}x_{13} + k_{21}x_{22} + k_{22}x_{23} + b\\ z_{21} = k_{11}x_{21} + k_{12}x_{22} + k_{21}x_{31} + k_{22}x_{32} + b\\ z_{22} = k_{11}x_{22} + k_{12}x_{23} + k_{21}x_{32} + k_{22}x_{33} + b \end{aligned} $$As for $\frac{\partial L}{\partial K}$, we can use the chain rule to get:
$$ \begin{equation} \frac{\partial L}{\partial b} = \sum_{i,j} \frac{\partial L}{\partial Z_{ij}} \frac{\partial Z_{ij}}{\partial b} \end{equation} $$However, differentiating the equations for $Z_{ij}$ with respect to $b$ gives us
$$ \frac{\partial Z_{ij}}{\partial b} \equiv 1 $$i.e.
$$ \frac{\partial L}{\partial B} = \sum_{i,j} \frac{\partial L}{\partial Z_{ij}} = \operatorname{Sum}\left( \frac{\partial L}{\partial Z}\right) $$where $\operatorname{Sum}()$ adds all the entries in the matrix.
Finding $\frac{\partial L}{\partial X}$
Finally, let’s find how the loss changes with respect to the input to the convolutional layer. This is necessary, as this allows us to follow the same process for the layer that feeds into this layer (i.e. propagating the error backwards)
Again, let’s first recall how the convolution operation creates each output. For our 2x2 kernel, each output element is calculated as:
$$ \begin{aligned} z_{11} &= k_{11}x_{11} + k_{12}x_{12} + k_{21}x_{21} + k_{22}x_{22}+ b \\ z_{12} &= k_{11}x_{12} + k_{12}x_{13} + k_{21}x_{22} + k_{22}x_{23}+ b \\ z_{21} &= k_{11}x_{21} + k_{12}x_{22} + k_{21}x_{31} + k_{22}x_{32}+ b \\ z_{22} &= k_{11}x_{22} + k_{12}x_{23} + k_{21}x_{32} + k_{22}x_{33} + b \end{aligned} $$Now, to find how changing an input pixel affects the loss, we need to consider all the output elements that use that input pixel in their calculation. For example, $x_{22}$ appears in all four equations above:
- In $z_{11}$ it’s multiplied by $k_{22}$
- In $z_{12}$ it’s multiplied by $k_{21}$
- In $z_{21}$ it’s multiplied by $k_{12}$
- In $z_{22}$ it’s multiplied by $k_{11}$
Similarly to with the kernel, using the chain rule, we sum up all these paths to get
$$ \left(\frac{\partial L}{\partial X}\right)_{mn} = \sum_{i,j} \frac{\partial L}{\partial Z_{ij}} \frac{\partial Z_{ij}}{\partial X_{mn}} $$We can do this for each input element, going through the expanded equations for $Z_{ij}$ differentiating each with respect to that input element, and plugging into the chain rule sum to get:
$$ \begin{bmatrix} \frac{\partial L}{\partial Z_{11}}k_{11} & \frac{\partial L}{\partial Z_{11}}k_{12} + \frac{\partial L}{\partial Z_{12}}k_{11} & \frac{\partial L}{\partial Z_{12}}k_{12} \\[0.2cm] \frac{\partial L}{\partial Z_{11}}k_{21} + \frac{\partial L}{\partial Z_{21}}k_{11} & \frac{\partial L}{\partial Z_{11}}k_{22} + \frac{\partial L}{\partial Z_{12}}k_{21} + \frac{\partial L}{\partial Z_{21}}k_{12} + \frac{\partial L}{\partial Z_{22}}k_{11} & \frac{\partial L}{\partial Z_{12}}k_{22} + \frac{\partial L}{\partial Z_{22}}k_{12} \\[0.2cm] \frac{\partial L}{\partial Z_{21}}k_{21} & \frac{\partial L}{\partial Z_{21}}k_{22} + \frac{\partial L}{\partial Z_{22}}k_{21} & \frac{\partial L}{\partial Z_{22}}k_{22} \end{bmatrix} $$Notice that the edges have fewer terms in the equation? Imagine you are $x_{11}$. The only time you are used in the computation of $Z$ is the first step of the convolution (when the kernel is in the top left corner). But if you are $x_{22}$, you are involved in every step of the convolution, so you impact $Z$ and therefore the loss in more ways so the gradient term is more complex.
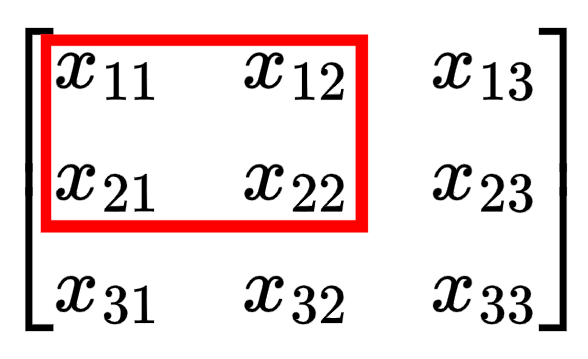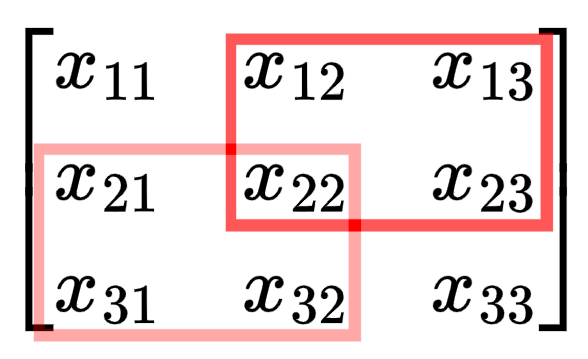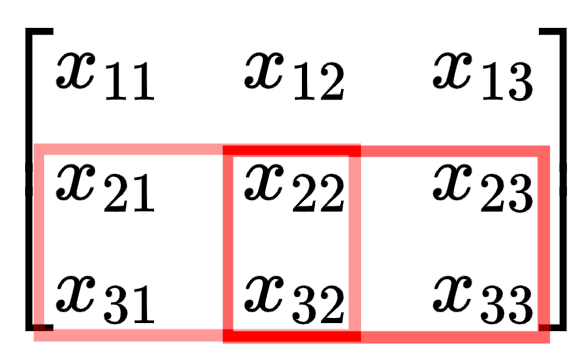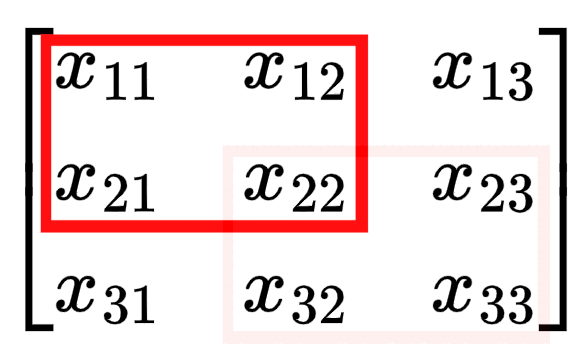
For a 2x2 kernel like in our example, the corners elements of the input matrix have 1 term in their gradient (affects 1 term of $Z$ and thus the gradient), the edges have 2 terms in their gradient (affects 2 terms of $Z$ and thus the gradient), and all other elements have 4 terms in their gradient (affect 4 terms of $Z$ and thus the gradient).
But back to $\frac{\partial L}{\partial X}$. You may struggle to see the pattern, but get out a piece of paper and expand the following
$$ \operatorname{Conv}\left( \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}} & 0 \\ 0 & \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} , \begin{bmatrix} k_{22} & k_{21} \\ k_{12} & k_{11} \end{bmatrix} \right) $$This indeed gives us the matrix for $\frac{\partial L}{\partial X}$, so
$$ \frac{\partial L}{\partial X} = \operatorname{Conv}\left( \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & \frac{\partial L}{\partial Z_{11}} & \frac{\partial L}{\partial Z_{12}} & 0 \\ 0 & \frac{\partial L}{\partial Z_{21}} & \frac{\partial L}{\partial Z_{22}} & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} , \begin{bmatrix} k_{22} & k_{21} \\ k_{12} & k_{11} \end{bmatrix} \right) = \operatorname{Conv}\left(\operatorname{Pad}\left(\frac{\partial L}{\partial Z}\right),\; K_{rot180°}\right) $$where $K_{rot180°}$ is the kernel rotated 180 degrees:
$$ K_{rot180°} = \begin{bmatrix} k_{22} & k_{21} \\ k_{12} & k_{11} \end{bmatrix} $$And $\operatorname{Pad}$ pads the matrix with the appropriate number of zeros for our kernel size.
This completes our derivation of the three key backpropagation equations for convolutional layers:
$$\frac{\partial L}{\partial X} = \operatorname{Conv}\left(\operatorname{Pad}\left(\frac{\partial L}{\partial Z}\right), K_{rot180°}\right)$$ $$\frac{\partial L}{\partial K} = \operatorname{Conv}\left(X, \frac{\partial L}{\partial Z}\right)$$ $$\frac{\partial L}{\partial b} = \operatorname{Sum}\left(\frac{\partial L}{\partial Z}\right)$$Conclusion
The above focused on a simple example; the input matrix was small, it only had a single channel, and there was no mention of passing the loss through the activation function to get $\frac{\partial L}{\partial Z}$ from $\frac{\partial L}{\partial A}$.
However, extending this notion to multiple channels is not conceptually difficult and can always be brought down to sums of these simple single-channel operations, and propagating the loss through the activation function is exactly the same as in an MLP (and thoroughly explained elsewhere).
This article should bring some understanding about why the equations of backpropagation for CNNs are the way that they are, not a step-by-step guide on how to implement the full backwards pass through the CNN; although this may be coming soon!